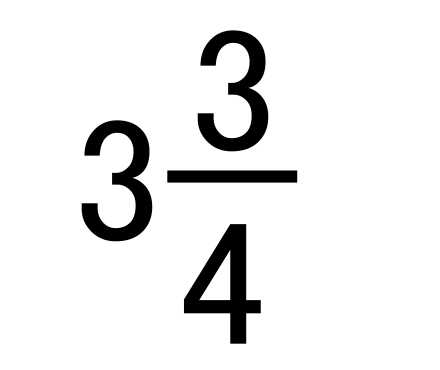分数

Entity大约 5 分钟

分数

分数的加减乘除运算

分数加法、分数减法、分数除法和分数乘法是四种基本的分数运算，让我为你详细解释每种运算：

分数加法：要将两个分数相加，首先确保它们的分母相同。如果分母相同，只需将分子相加，然后将结果的分子写在分母下方。如果分母不同，需要找到一个公共分母，然后将两个分数都转化为具有该公共分母的分数，然后再相加。例如：
- 加法示例：1/3 + 1/4 = (4/12) + (3/12) = 7/12。
- 相关信息
  当进行分数加法时，关键是确保两个分数的分母相同。如果分母相同，只需将分子相加即可。如果分母不同，你需要找到一个公共分母，然后将两个分数都转化为具有该公共分母的分数，再相加。以下是详细的分数加法示例：
  假设你要计算 1/3 + 2/5。
  步骤 1：找到公共分母首先，查看两个分数的分母。在这个例子中，一个分数的分母是3，另一个分数的分母是5。要执行加法，你需要找到这两个分母的公共倍数，作为新的公共分母。
  3 和 5 的最小公共倍数是 15，所以我们将选择 15 作为新的公共分母。
  步骤 2：将分数转化为具有公共分母的分数现在，我们需要将这两个分数都转化为具有公共分母 15 的分数。
  - 对于 1/3，我们将分子和分母都乘以 5，以得到具有分母 15 的分数：(1/3) * (5/5) = 5/15。
  - 对于 2/5，我们将分子和分母都乘以 3，以得到具有分母 15 的分数：(2/5) * (3/3) = 6/15。
  现在，两个分数都具有相同的分母 15。
  步骤 3：将分数相加现在，我们可以将这两个分数相加，因为它们具有相同的分母。
  (5/15) + (6/15) = (5 + 6) / 15 = 11/15。
  所以，1/3 + 2/5 = 11/15。
分数减法：分数减法的原则与分数加法相似。首先确保分母相同，然后将分子相减。如果分母不同，需要找到一个公共分母，然后将两个分数都转化为具有该公共分母的分数，然后再相减。例如：
- 减法示例：5/8 - 1/4 = (5/8) - (2/8) = 3/8。
分数除法：分数除法涉及将一个分数除以另一个分数。要执行分数除法，你需要将除法转化为乘法，即将被除数与倒数（除数的分子和分母互换位置）相乘。例如：
- 除法示例：(2/3) ÷ (1/4) = (2/3) * (4/1) = 8/3。
分数乘法：分数乘法是将两个分数相乘，将它们的分子相乘并将分母相乘。例如：
- 乘法示例：(2/5) * (3/4) = (2 * 3) / (5 * 4) = 6/20，通常需要将结果简化为最简分数，即 3/10。

这些是四种基本的分数运算。要执行这些运算，首先确保分数的分母相同，然后进行相应的数学操作。如果分母不同，需要找到公共分母，然后将分数转化为具有相同分母的分数，然后再进行操作。

带分数

带分数（mixed number）是一个混合表示方式，它包括一个整数部分和一个分数部分。带分数用于表示一个整数和一个小于1的分数的组合。通常，带分数的形式如下：

整数部分分数部分

例如，带分数 "3 1/2" 表示3个整数和1/2（半）的分数部分。这表示总共有3个整数和半的部分，等于3.5。带分数通常在日常生活中用于表示某些度量或数量，使信息更直观和易于理解。

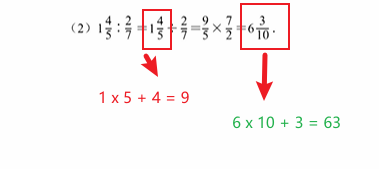
带分数可以转化为纯分数形式，以便进行数学运算。例如，带分数 "3 1/2" 可以转化为纯分数 "7/2"，这是3倍2加上1，然后分母保持不变。带分数提供了一种更友好的方式来表示分数，特别是在非形式的环境中。

分数

# 分数

# 分数的加减乘除运算

# 带分数

分数

分数的加减乘除运算

带分数